传说中的小学数学题--求阴影面积

传说中的小学数学题--求阴影面积进入全屏

一、题目

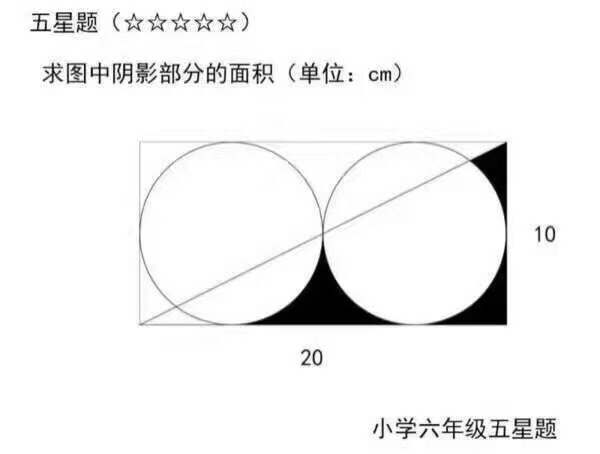
shadow.pic副本.jpg

二、解答

这是小学题？我简直不相信。。。不过我对这种东西还是蛮感兴趣的，可惜。。。什么三角函数之类的，现在全都忘了，只能问度娘！在网上看到一个类似的，我来照着这个辅助图推理一下

1、作辅助线如上

2、分解计算

S阴影 = 阴影面积计算推理

S阴影 = ( S长方形 - 2 * S圆 ) / 2 - S左下角白色小三角
     = ( S长方形 - 2 * S圆 ) / 2 - ( ( S长方形 - S圆 ) / 8 - S阴影ABC )
     = ( S长方形 - 2 * S圆 ) / 2 - ( S长方形 - S圆 ) / 8 + S阴影ABC
     = 3 * ( S长方形 - 2 * S圆 ) / 8 + S阴影ABC
     = 3 * ( S长方形 - 2 * S圆 ) / 8 + ( S三角形ABC - S红色小块 )
     = 3 * ( S长方形 - 2 * S圆 ) / 8 + ( S三角形ABC - ( S扇形BOC - S三角形OBC ) )
     = 3 * ( S长方形 - 2 * S圆 ) / 8 + ( S三角形ABC - ( S扇形BOC - S三角形OBC ) )

S长方形 = 长方形面积计算推理

S长方形 = W长方形 * H长方形 = 20 * 10 = 200 (cm²)

S圆 = 圆形面积计算推理

S圆 = π * r圆半径² = π * 5² 
    = 25π 
    = 78.53981633974483 (cm²)

S三角形ABC = 三角形ABC面积计算推理

∵ tan∠BAC = 对边  / 临边 = BC / AC 
∵ tan∠BAC = 对边  / 临边 = 2 * OB / AB = 2 * 5 / 5 = 2
∴ BC / AC = 2
∴ BC = 2 * AC
∵ AB² =  BC² + AC² = ( 2 * AC )² + AC² = 5 * AC² 
∴ AC =  AB / √5 = 5 / √5  = √5 

S三角形ABC = AC * BC / 2 = AC * 2 * AC / 2 = AC² = 5

S三角形OBC = 三角形OBC面积计算推理

∵ △BOC是等腰三角形
∵ AB = OB
∴ 三角形ABC 和 三角形OBC的一半儿 是全等三角形

S三角形OBC = 2 * S三角形ABC = 2 * 5 = 10 (cm²)

S扇形BOC = 扇形OBC面积计算推理

∵ tanα = tan∠ABC = 对边 / 临边 = AC / BC = 0.5
∴ α = arctan(0.5) 

S扇形BOC = 2 * α / ( 2 * π ) * S圆 
        = α / π * S圆
        = arctan(0.5) / π * 25π
        = 25 * arctan(0.5)
        = 25 * Math.atan(0.5)
        = 25 * 0.46364760900080615
        = 11.591190225020153 (cm²)

3、结果汇总

S阴影 = 3 * ( S长方形 - 2 * S圆 ) / 8 + ( S三角形ABC - ( S扇形BOC - S三角形OBC ) )
     = 3 * ( 200 - 2 * 78.53981633974483 ) / 8 + ( 5 - ( 11.591190225020153 - 10 ) )
    = 19.503947520171224 (cm²)

其实我也不知道这结果到底算不算对！

三、代码实现

比我还无聊的 @张四哥用代码暴力验证一下我的结果。。。跪了！用到的算法是「1946年的蒙特卡洛方法」：

[1946: John von Neumann, Stan Ulam, and Nick Metropolis, all at the Los Alamos Scientific Laboratory, cook up the Metropolis algorithm, also known as the Monte Carlo method.]

...

1946年，美国拉斯阿莫斯国家实验室的三位科学家John von Neumann,Stan Ulam 和 Nick Metropolis共同发明，被称为蒙特卡洛方法。

它的具体定义是：

在广场上画一个边长一米的正方形，在正方形内部随意用粉笔画一个不规则的形状，现在要计算这个不规则图形的面积，怎么计算列?蒙特卡洛(Monte Carlo)方法告诉我们，均匀的向该正方形内撒N（N 是一个很大的自然数）个黄豆，随后数数有多少个黄豆在这个不规则几何形状内部，比如说有M个，那么，这个奇怪形状的面积便近似于M/N，N越大，算出来的值便越精确。在这里我们要假定豆子都在一个平面上，相互之间没有重叠。

...

蒙特卡洛方法可用于近似计算圆周率：让计算机每次随机生成两个0到1之间的数，看这两个实数是否在单位圆内。生成一系列随机点，统计单位圆内的点数与总点数，（圆面积和正方形面积之比为PI:1，PI为圆周率），当随机点取得越多（但即使取10的9次方个随机点时，其结果也仅在前4位与圆周率吻合）时，其结果越接近于圆周率。

Js版本代码：

/**
 * 给图形画一个坐标,检测(x,y)点是否落入阴影区域部分
 * @param {float} x 横坐标
 * @param {float} y 纵坐标
 * @returns {boolean} 落入阴影:true,否则:false
 */
var detectFallIn = function (x, y) {

    return (x / y < 2 || x < 5) ? false :
        (Math.sqrt(Math.pow(x - 5, 2) + Math.pow(y - 5, 2)) >= 5 &&
        Math.sqrt(Math.pow(x - 15, 2) + Math.pow(y - 5, 2)) >= 5);
};

/**
 * 利用「蒙特卡洛方法」计算阴影(不规则图形)部分的面积
 * @param {int} soyaNums 黄豆的数量
 */
var calShadowArea = function (soyaNums) {
    var x, y, fallIn = 0;
    for (var i = 0; i <= soyaNums; i++) {
        // 将黄豆随机洒落到长方形中
        x = Math.random() * 20;
        y = Math.random() * 10;

        // 判断黄豆是否落入阴影区域
        if (detectFallIn(x, y)) {
            fallIn++;
        }
    }

    // 阴影面积
    var shadow = 20 * 10 * (fallIn / soyaNums);
    console.log('shadow area = ', shadow);
};

算法表示，种子越多，结果越精确，所以，尝试用一千万颗黄豆来做这个实验：

// 假设用1kw颗黄豆做实验
calShadowArea(10000000);

得到结果（每次执行都会得到一个近似值，毕竟是随机数来计算的）：

屏幕快照 2016-08-04 下午3.37.52.png

四、总结

这两天脑子转的慢，做做「小学」数学题，开开脑洞，保持清醒！

发表于：2016-08-03 19:07:19 #数学题 #阴影面积 #蒙特卡洛